Introduction
Hydrus-1D is a widely used numerical model developed for simulating water, heat, and solute movement in variably saturated porous media such as soil and hydroponic substrates. Its primary focus is on solving the Richards equation for unsaturated flow, and it is capable of handling a wide variety of soil profiles and boundary conditions, making it an essential tool for researchers and engineers in the fields of hydrology,
soil science, and environmental engineering. One of the key applications of Hydrus-1D is the simulation of soil moisture profiles, where it models the distribution of water content through soil layers under
various conditions of infiltration, evaporation, and root uptake, providing detailed insights into the subsurface flow processes (Šimůnek et al., 2008).
Despite its robust capabilities for simulating single runs with precise control over soil hydraulic properties and boundary conditions, Hydrus-1D was not originally designed to support multiple simulations in a Monte Carlo framework. This limitation poses challenges for users who wish to assess the impact of uncertainty in soil parameters, such as hydraulic conductivity ($Ks$) or soil water retention characteristics, on the simulated soil profiles (e.g. Kontaxakis et al., 2023, Papadimitriou et al., 2024). In such cases, researchers often need to develop custom scripts or workflows such as the one provided by Groenendyk (2014) and Diamantopoulos (2017) for MATLAB. Packages hydrusR (Acharya, 2020) and RHydrus (Temple Lang, 2023) may also support such workflows in R.
Methodology
Hydrus 1D
Hydrus-1D solves the Richards equation for water flow in unsaturated soils, incorporating the van Genuchten-Mualem (vG-Mualem) equation to describe the soil-water retention curve and hydraulic conductivity as a function of soil moisture content. The vG-Mualem model is widely used for describing the hydraulic properties of unsaturated porous media. The soil-water retention function is given by:
$$
\theta(h) = \theta_r + \frac{\theta_s – \theta_r}{\left(1 + | \alpha h |^n \right)^m}
$$
where $\theta(h)$ is the volumetric water content at a given matric potential $h$, $\theta_r$ and \$ _s \$ are the residual and saturated water contents, respectively, $\alpha$ is a parameter related to the
inverse of the air-entry suction, and $n$ and $m$ are empirical shape parameters with $m = 1 – 1/n$.
The unsaturated hydraulic conductivity $K(\theta)$ is described by the Mualem conductivity model:
$$
K(\theta) = K_s S_e^{l} \left[ 1 – \left( 1 – S_e^{1/m} \right)^m \right]^2
$$
where $K_s$ is the saturated hydraulic conductivity, $l$ is an empirical pore-connectivity parameter, and $S_e$ is the effective saturation given by:
$$
S_e = \frac{\theta – \theta_r}{\theta_s – \theta_r}
$$
The van Genuchten-Mualem model allows Hydrus-1D to simulate complex soil-water dynamics with high accuracy across a wide range of soil types and conditions (van Genuchten, 1980; Mualem, 1976). By incorporating these equations, Hydrus-1D can model water flow in variably saturated soils, accounting for the nonlinear relationship between soil moisture, matric potential, and hydraulic conductivity.
Automation in R
Here I use an R Quarto (R Core Team, 2021) script as a wrapper to automate and manage multiple Hydrus-1D simulations. This approach involves generating a separate directory for each simulation, with each directory containing edited input files (Selector.in, Atmosph.in, and PROFILE.dat) tailored to different soil hydraulic parameters. After preparing the input files, Hydrus-1D is executed from the command line
using R’s system function, which enabled the seamless integration of the external model into the R environment. The script supports both single-processor execution for sequential runs and parallel processing to accelerate the simulations using the parallel package (R Core Team, 2021). Once the simulations are completed, the results are collected and visualized using the ggplot2 package (Wickham, 2016). This allows for the generation of plots illustrating soil moisture profiles over time, facilitating the comparison of different scenarios and their outcomes under varying soil conditions. The script can be found in Daliakopoulos (2024).
Case study
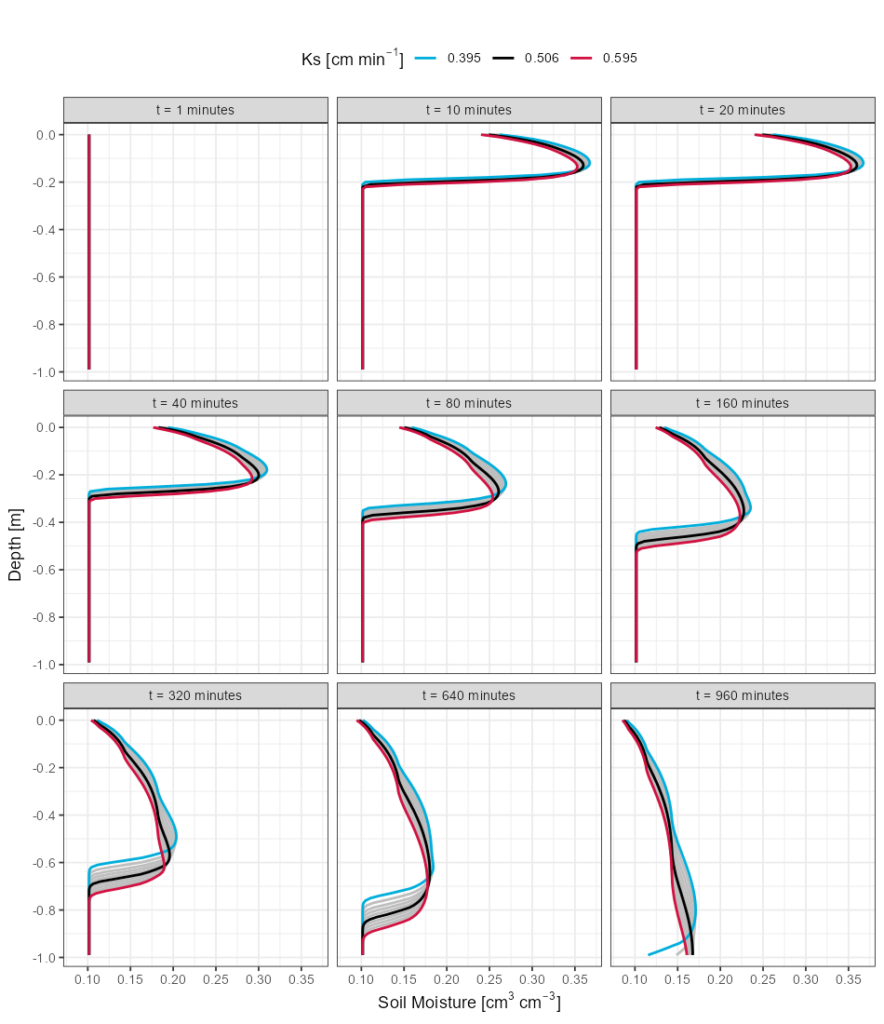
Let’s assume a 100 cm deep profile of sandy soil ($\theta_r$ = 0.045 $cm^3 cm^{-3}$, $\theta_s$ = 0.43 $cm^3 cm^{-3}$, $\alpha$ = 0.145 $cm^{-1}$, $n$ = 2.68, $l$ = 0.5, and $K_s$ = 0.495 $cm~min^{-1}$ with a variance of 0.3 $cm min^{-1}$). Given a 10-minute irrigation event of 1 $cm min^{-1}$. 10 simulations along the range of $K_s$ provide enough data to visualise the range of $\theta$ throughout the soil profile. Figure 1 shows the value of $\theta$ for 9 timesteps (1, 10, 20, …, and 960 minutes) picked across the simulations.
Conclusions and next steps
The script facilitates the visualisation of HYDRUS-1D results for simple simulations of water trasnport is soils. Including more formal read/write functions from the hydrusR package (Acharya, 2020) will allow for higher diversity in the scenarios that can be simulated.
References
Daliakopoulos, I. (2024). hydrus-soil-profile. Accessible online: https://github.com/daliakopoulos/hydrus-soil-profile
Diamantopoulos, E. (2017). Running Hydrus (1D) in Matlab, PC-PROGRESS. Accessible online:
https://www.pc-progress.com/Downloads/Tutorials/Matlab_RunningHydrus.pdf
Groenendyk, D. (2014). hydrus-batch-matlab. Accessible online: https://github.com/MoonRaker/hydrus-batch-matlab
Kontaxakis, E., Papadimitriou, D., Daliakopoulos, I., Sabathianakis, I., Stavropoulou, A., & Manios, T. (2023). Water Availability in Pumice, Coir, and Perlite Substrates Regulates Grapevine Growth and Grape Physicochemical Characteristics in Soilless Cultivation of Sugraone and Prime Cultivars (Vitis vinifera L.). Agriculture, 13(9), 1690.
Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12(3), 513-522.
Papadimitriou, D. M., Daliakopoulos, I. N., Louloudakis, I., Savvidis, T. I., Sabathianakis, I., Savvas, D., & Manios, T. (2024). Impact of container geometry and hydraulic properties of coir dust, perlite, and
their blends used as growing media, on growth, photosynthesis, and yield of Golden Thistle (S. hispanicus L.). Scientia Horticulturae, 323, 112425.
R Core Team (2021). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria.
Šimůnek, J., Šejna, M., & van Genuchten, M. T. (2008). The Hydrus-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media. U.S. Salinity Laboratory,
USDA, Riverside, California.
Acharya, S. (2020). hydrusR. Available online: https://github.com/shoebodh/hydrusR
Temple Lang, D. (2023). RHydrus. Available online: https://github.com/mespe/RHydrus
van Genuchten, M. Th. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892-898.
Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York.

